基本概念
当无法用代数方法积分函数时,可以使用数值方法来近似计算曲线下的面积。
梯形法则:\(\int_a^b y dx \approx \frac{1}{2}h[y_0 + 2(y_1 + y_2 + ... + y_{n-1}) + y_n]\)
其中:\(h = \frac{b-a}{n}\),\(y_i = f(a + ih)\)
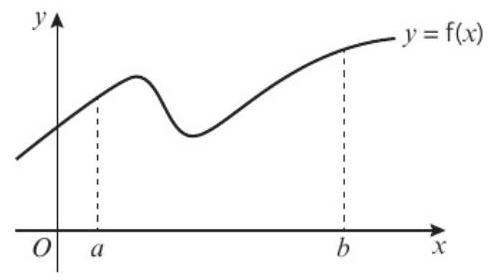
图1:梯形法则基本概念
计算步骤
1. 确定分割数:选择n值,计算h = (b-a)/n
2. 计算x值:x = a, a+h, a+2h, ..., b
3. 计算y值:y = f(x) 在每个x点的值
4. 制作表格:列出所有x和y值
5. 应用公式:使用梯形法则公式计算
6. 检查精度:增加分割数可提高精度
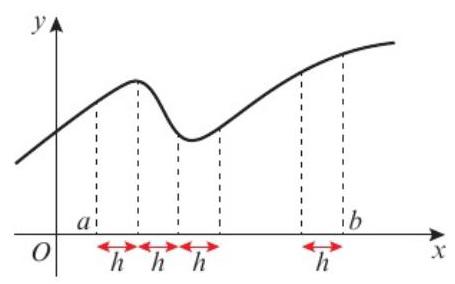
图2:梯形分割示意图
梯形面积公式
每个梯形的面积 = \(\frac{1}{2}(y_0 + y_1)h\)
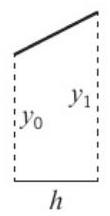
图3:单个梯形面积计算
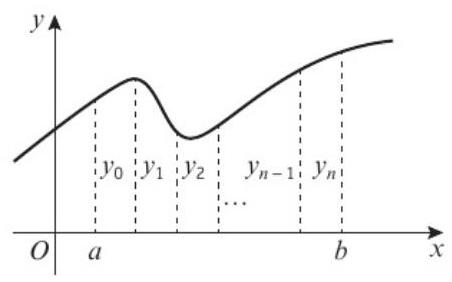
图4:多个梯形组合近似曲线下面积
Example 10 - 梯形法则应用
题目:Use the trapezium rule with 4 strips to estimate the area under \(y = \sqrt{2x + 3}\) between x = 0 and x = 2.
解:
h = (2-0)/4 = 0.5
| x | 0 | 0.5 | 1 | 1.5 | 2 |
|---|
| y = √(2x + 3) | 1.732 | 2 | 2.236 | 2.449 | 2.646 |
|---|
Area = ½ × 0.5 × (1.732 + 2(2 + 2.236 + 2.449) + 2.646)
= 0.25 × 17.748 = 4.437
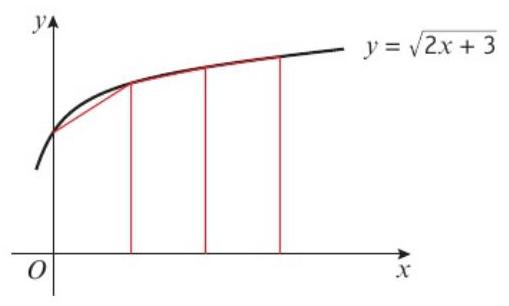
图5:Example 10 - y = √(2x + 3) 曲线图
精度分析
凹曲线:当曲线是凹的(向下弯曲)时,梯形完全在曲线下方,梯形法则会给出低估值。
提高精度:增加梯形数量(减少宽度)可以提高近似的精度。
重要提示
• 对于n个梯形,将有n+1个x值和n+1个y值
• 在考试中要显示x_i和y_i的值以及如何代入公式
• 计算器通常使用与梯形法则略有不同的方法
练习题精选
1. \(\int_1^3 \frac{1}{x^2 + 1} dx\) ≈ 0.473
2. \(\int_1^{2.5} \sqrt{2x - 1} dx\) ≈ 2.331
3. \(\int_0^2 \sqrt{x^3 + 1} dx\) ≈ 3.139
4. \(\int_1^3 \frac{1}{\sqrt{x^2 + 1}} dx\) ≈ 0.939
5. \(\int_{-1}^1 \frac{1}{x + 2} dx\) ≈ 1.111(高估值)
常见错误
• 忘记制作表格
• y_0和y_n的系数错误
• 中间y值的系数错误
• 计算精度不够
解题技巧
• 总是制作表格列出x和y值
• 注意公式中y_0和y_n的系数是1
• 中间y值的系数是2
• 检查计算精度




